Introducción
Contenidos
En este artículo se muestra cómo hacer una predicción de la tasa de crecimiento mensual del IMACEC cuando tenemos muchas variables disponibles, y no sabemos cuáles son las mejores predictoras del IMACEC. Este problema se puede solucionar de forma automática, usando métodos de machine learning.
El código utilizado en este artículo se puede encontrar en GitHub.
Variable dependiente
En este ejemplo la variable dependiente fue la primera diferencia del IMACEC, es decir:

Predictores
Se utilizaron como predictores los siguientes índices de percepciones: indicador mensual de confianza empresarial (IMCE), índice de confianza empresarial (ICE), índice de percepción del consumidor (IPECO), índice de percepción de la economía (IPEC), índice de incertidumbre económica (IEC).
Además, se usaron las siguientes variables, obtenidas de la base de datos estadísticos del Banco Central: IPSA, M1, M2, M3, Colocaciones reales, Colocaciones Consumo, Colocaciones Vivienda, Colocaciones Comerciales, Precio del cobre, Precio del petróleo WTI, Spread EMBI Chile, Bono de gobierno a 10 años – EE.UU., Índice de producción industrial INE, Índice de producción Minería, Índice de producción Manufacturera, Despacho de energía eléctrica CDEC (GWh), Ventas autos nuevos ANAC, IPC General, IPC SAE, IPC sin volátiles, Fuerza de trabajo, Empleo, Tasa de desempleo, TCN, TPM, Tasas BCP 2 años, Tasas BCP 5 años, Tasas BCP 10 años, Tasas BCU 2 años, Tasas BCU 5 años, Tasas BCU 10 años.
Por último, se usaron como predictores el primer rezago de la variable dependiente, y el rezago de 12 meses atrás (para capturar efectos estacionales).
En total suman 38 variables.
Todas las variables se transformaron a la primera diferencia.
Análisis de correlaciones
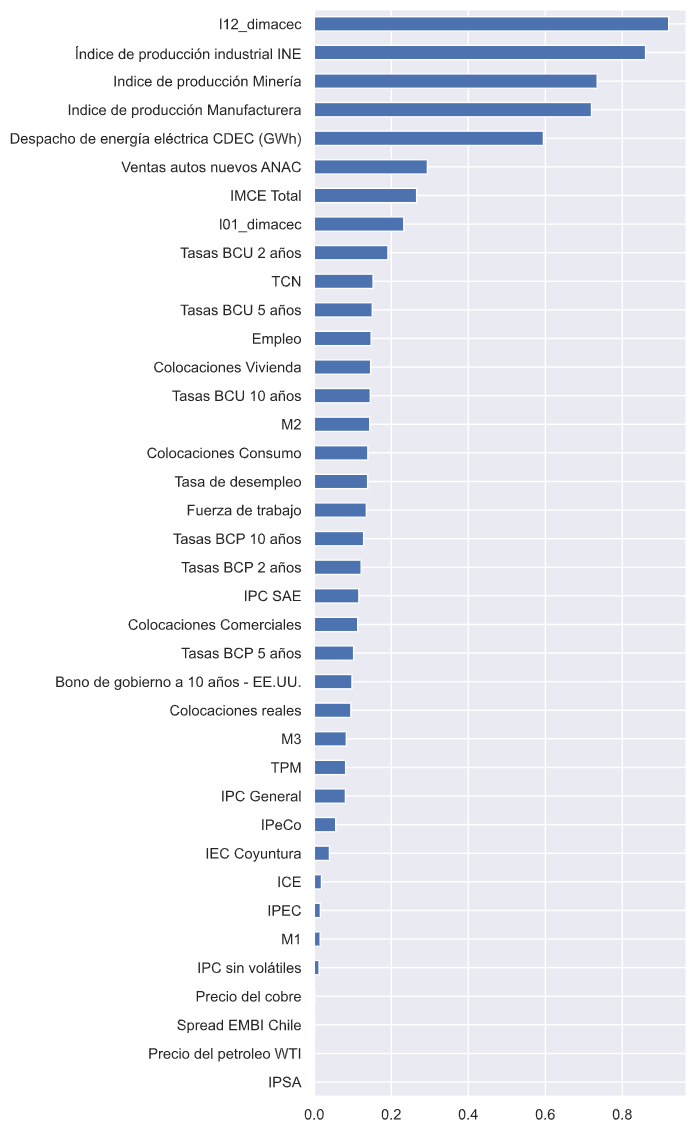
En el siguiente gráfico se muestran las correlaciones, en valor absoluto, ordenadas de mayor a menor. La tres variables más correlacionadas con el crecimiento mensual del IMACEC son: el rezago de 12 meses atrás, el índice de producción industrial del INE, y el índice de producción industrial de la minería. Entre los índices de percepciones, la mayor correlación se da con el IMCE.
Training y Testing sets
A continuación se dividió la base de datos en dos conjuntos, uno para entrenar los modelos (hacer estimaciones) y otro para testearlos (hacer predicciones fuera de la muestra y calcular métricas de error).
El conjunto de entrenamiento abarcó el periodo 2010-04 a 2017:12. Durante este periodo se cuenta con observaciones para todas las variables. En total se cuentan 93 meses.
El conjunto de testeo abarcó el periodo 2008-01 a 2021:09. Este periodo incluye los años más recientes, en que la economía se ha visto afectada por la pandemia de covid19. El periodo suma 45 meses.
Estandarización de variables
El siguiente paso fue estandarizar las variables predictoras. Esto se hace debido a que algunos algoritmos de optimización de los modelos son sensibles a la escala de las variables. Por esta razón, estandarizar permite lograr mejores y más rápidos resultados.
Se estandarizó el conjunto de variables predictoras usando la media y varianza del train set. En otras palabras, tanto los datos del train set como los del test set se estandarizaron con los parámetros estimados a partir de datos del train set, exclusivamente, para no contaminar el train set con información del test set.
La variable dependiente no se estandarizó.
Métricas de error
Se calcularon 4 métricas de error:
- RMSE_CV. Raíz del error cuadrático medio de cross-validation. Raíz cuadrada del promedio de los errores de predicción al cuadrado, calculados usando cross validation (estimación del error fuera de la muestra usando datos del train set).
- RMSE_Test. Raíz del error cuadrático medio del test set.
- MAE_Test. Error absoluto medio del test set. Promedio de los errores de predicción en valor absoluto. Es una métrica que se puede interpretar directamente como el margen de error de la predicción, y, además, es robusta a outliers en los errores.
- R2_Test. R2 del test set, que se puede interpretar como una medida estandarizada del MSE. Los valores se distribuyen entre 0 y 1, donde los valores más cercanos a 1 indican un menor MSE (mejor predicción).
Modelos
Se usaron los siguientes modelos:
- Linear Regression. Regresión lineal clásica, que se utilizó como referencia para comparar los resultados de los demás modelos. Se usaron las 38 variables como predictoras (más intercepto).
- Elastic Net. Regresión lineal con método de regularización Elastic Net, que combina los métodos Lasso (L1) y Ridge (L2). La regularización implica estimar los coeficientes restringiendo los valores que pueden tomar. De esta forma se reduce la varianza de la predicción, que es uno de los componentes del error de predicción.
- Bagging. Método de ensemble learning, que combina las predicciones de otros modelos (modelo base). Cada modelo base se estima usando una muestra aleatoria de datos, obtenida mediante Bootstrap. En este ejemplo se combinaron las predicciones de modelos Elastic Net, y, además, en cada modelo base se utilizó un subconjunto aleatorio de variables predictoras.
- Random Forest. Modelo de ensemble en que el modelo base es un Decision Tree (árbol de decisión). Es un caso particular de Bagging. Tanto las muestras como las variables predictoras se seleccionan aleatoriamente.
- XGBoost. Modelo de ensemble learning en que se combinan las predicciones de modelos de árbol de forma secuencial. En cada iteración, los errores de predicción del modelo anterior se convierten en la variable dependiente del siguiente modelo.
- Stacking. Modelo de ensemble en que se combinaron las predicciones de todos los modelos anteriores. El metamodelo usa como variables tanto las predicciones de los otros modelos, como las 38 variables predictoras originales. El metamodelo utilizado fue del tipo XGBoost.
Cada modelo depende una serie de hiper parámetros exógenos, cuya elección se hizo mediante una búsqueda de grilla, de forma tal de optimizar el RMSE de cross validation. Así se evitó seleccionar dichos parámetros de forma arbitraria, a la vez que se mejoró la precisión de la predicción.
Resultados
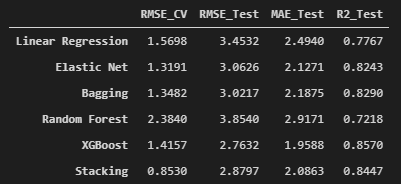
En el siguiente cuadro se muestran los resultados para las métricas de error. Se encuentra que el mejor modelo en términos de RMSE_CV fue el Stacking, pero en todas las métricas calculadas en el test set, el mejor modelo fue XGBoost.
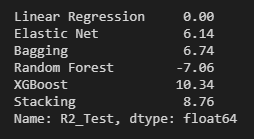
En el siguiente cuadro se muestra la columna del R2_test, en que cada valor se dividió por el valor del R2_Test de la Linear Regression y se multiplicó por 100. Se observa que XGBoost mejoró el R2_Test en un 10.34% (en relación al R2_Test de la regresión lineal).
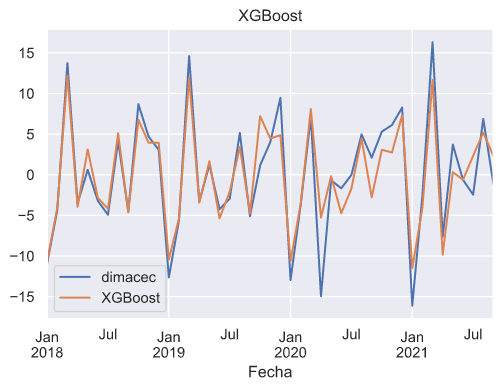
En el siguiente gráfico se muestra la predicción del modelo XGBoost en el test set (predicción fuera de la muestra). Se observa que el resultado es muy bueno, incluso durante los meses de pandemia, en que el IMACEC creció a tasas pocas veces registradas.

Comentarios finales
Los modelos y herramientas de machine learning tienen muchas aplicaciones prácticas en economía, sobre todo al hacer predicciones. Sin embargo, estos modelos tienen ciertas debilidades, ya que, por ejemplo, no permiten hacer estimaciones estructurales, hacer inferencia o identificar relaciones causales. Por otro lado, en algunos casos, los parámetros estimados por los modelos no tienen una interpretación clara, o es difícil explicar cómo se generan las predicciones (se dice que son como una caja negra).
Pese a estas dificultades, es importante considerar estos modelos como parte del arsenal econométrico de los economistas modernos, ya que, aunque no se puedan usar como sustitutos de los modelos econométricos clásicos, son excelentes complementos.