Introducción ¿Por qué aleatorizar?
Contenidos
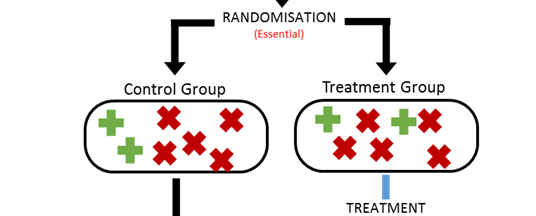
Antes de hacer un experimento aleatorio controlado, los participantes son asignados aleatoriamente a los grupos de tratamiento y control, para así obtener grupos que sean estadísticamente iguales tanto en sus características observables como inobservables. De esta manera, la única diferencia entre los grupos es el tratamiento, lo que permite identificar su efecto causal sobre las variables de resultado. En otras palabras, se logra validez interna.
¿Por qué aleatorizar estratificadamente?
La asignación aleatoria estratificada proporciona una forma de asegurar que los grupos de tratamiento y control estén equilibrados en lo que se refiere a las variables de más importancia. Por ejemplo, asegura que haya tantas mujeres como hombres, o que estos estratos se encuentren en la misma proporción que la población de origen.
Para hacer una asignación de este tipo, primero se divide un conjunto de unidades elegibles en estratos, y luego, dentro de cada estrato, se hace un muestreo aleatorio simple.
¿Cuándo estratificar?
Estratificar permite equilibrar, aumentar el poder estadístico y facilitar el análisis mediante subgrupos. Una razón no técnica es cumplir con las limitaciones del implementador o de las políticas.
En concreto, aleatorizar es útil:
Cuando se quiere tener equilibrio. Cuanto más pequeño sea el tamaño muestral, mayor será la probabilidad de que la aleatorización simple produzca grupos no equilibrados, y, por lo tanto, mayor será la necesidad de estratificación.
Cuando se quiere aumentar el poder estadístico. Estratificar en base a variables con gran poder de predicción del resultado puede aumentar el poder estadístico.
Cuando se quiere analizar el impacto por subgrupo. Si no, es posible terminar sin participantes suficientes en un subgrupo de interés.
Cuando es necesario equilibrar una muestra para facilitar la viabilidad política o logística. Estas razones a veces imponen estratificar geográficamente, por género, o por alguna variable relevante para los tomadores de decisiones de política.
¿Qué variables usar para estratificar?
Variables discretas. Si, en cambio, se desea estratificar en base a una variable continua, se debe hacer en base a un rango de dicha variable, es decir, transformándola en un conjunto de variables categóricas.
Variables muy correlacionadas con los resultados de interés. Estratificar por variables de confusión, es decir, aquellas variables altamente correlacionadas con el resultado final y la participación. Además, si está disponible en la línea de base, el valor de la variable de resultado que nos interesa también es una variable de estratificación muy importante (ya que se debería correlacionar con el resultado ex post).
Variables en las que se harán análisis de subgrupos. Por ejemplo, si se analizaran los subgrupos por género, debería estratificarse por género, para tener equilibrio en el género y aumentar al máximo el poder estadístico.
¿Con cuántas variables estratificar?
Tamaño del estrato. Si se intenta estratificar con demasiadas variables, puede encontrarse que se tienen estratos con una sola unidad, haciendo imposible la asignación a los grupos de tratamiento y control. Considerar que para estratificar se divide la muestra en subgrupos determinados por todas las variables utilizadas. Así, por ejemplo, si se estratifica por dos variables, con dos categorías cada una, se tendrán 4 subgrupos, con 3 variables se tendrán 8 subgrupos, etc. Deberían tenerse al menos tantas unidades en los estratos como celdas de aleatorización (si se tienen 2 grupos, T y C, se deberían tener al menos 2 unidades por estrato).
Practicabilidad. Cuanto mayor sea el número de variables de estratificación, tanto más difícil será lograr un equilibrio en todas ellas. Sobre todo cuando se tienen variables continuas, se enfrenta un tradeoff entre la obtención del equilibrio total en una variable (o pocas variables) o un equilibrio menos riguroso en muchas variables (es menos probable encontrar el equilibrio con variables continuas, ya que no se encontrarán los mismos valores en todos los estratos).
Poder estadístico. Cuando se tienen muchos subgrupos disminuye la varianza, pero se pierden grados de libertad debido a las mayores restricciones. El problema de tener muchos estratos es que potencialmente disminuyen los grados de libertad en el análisis final. En las regresiones los estratos deberían incluirse como variables dependientes (como variables dummy, aunque no hay consenso respecto de su necesidad), y al incluir muchas variables de estrato se reduce el poder estadístico.
Bibliografía
Glennerster, R., & Takavarasha, K. (2013). Running Randomized Evaluations: A Practical Guide. Princeton University Press. https://doi.org/10.2307/j.ctt4cgd52