Regresión cuantílica
Contenidos
La mayoría de los análisis econométricos se enfocan en los promedios, por ejemplo, si un programa de empleo en promedio aumenta el empleo, éste se considera efectivo. Sin embargo, hay casos en que la distribución de una variable puede cambiar de una forma tal que no es capturada por el promedio.
Un ejemplo que ilustra el fenómeno anterior se da al examinar los cambios en la distribución del ingreso, en la que el ingreso de los cuantiles más altos suele aumentar más rápidamente que el ingreso de los grupos menos privilegiados, provocando un aumento de la desigualdad. También podría suceder que el endeudamiento aumente en mayor proporción en los hogares de más bajos ingresos, mientras que en los hogares de altos ingreso se observa un ahorro neto.
De la misma manera, el efecto marginal de una variable sobre otra puede variar en distintos puntos de la distribución de la variable dependiente. Por ejemplo, la distribución condicional del ahorro (%) sobre el ingreso se observa mucho más comprimida en niveles bajo de ingreso que para los grupos más acomodados.
En qué se diferencia la regresión de cuantiles de la regresión lineal
El análisis de regresión lineal estándar permite revelar la relación promedio entre una variable dependiente y un conjunto de variables explicativas, mientras que, en contraste, la regresión de cuantiles es una herramienta que permite estimar la relación entre la variable independiente y los regresores en distintos puntos de la distribución condicional de la variable independiente, entregando una descripción más completa de las relaciones existentes.
Un ejemplo del uso de la regresión de cuantiles
En el ejemplo del gráfico, se estima una curva de Engel, es decir, una ecuación que estima la relación entre la cantidad demandada de un bien o servicio y el ingreso del consumidor. En particular, se estima la relación entre el gasto en salud y el gasto total de hogar. Los datos provienen de una encuesta realizada a 5.000 hogares de Vietnam, en 1997, en la que el gasto médico de estos hogares consiste principalmente en la adquisición de medicinas.
La estimación de una regresión lineal dio como resultado una elasticidad de 0.57, lo que se interpreta como una demanda inelástica, en otras palabras, la demanda de medicinas sería poco sensible a los cambios en el ingreso, debido a que se trata de una ‘necesidad’. En este contexto es interesante estudiar si existen diferencias en la elasticidad dependiendo del nivel de ingreso de los hogares, para lo cual es útil contar con una herramienta como la regresión de cuantiles.

El gráfico anterior muestra las líneas de regresión en los cuantiles 10, 50 (mediana) y 90. Se observa que efectivamente se producen diferencias en la estimación de la elasticidad para diferentes puntos de la distribución del ingreso. La pendiente de las líneas de regresión muestra que la elasticidad aumenta a medida que aumenta el ingreso. En el caso de los grupos de mayor ingreso, la elasticidad aumenta a 0.85, lo que implica que los hogares más pudientes aumentan su gasto en medicinas en mayor proporción cuando aumenta su ingreso que los grupos menos privilegiados.
Least Absolute Deviations (LAD)
El método conocido como Least Absoute Deviations (Mínimas Desviaciones Absolutas) es análogo a la estimación de Mínimos Cuadrados Ordinarios (MCO), pero en lugar de minimizar la suma de errores al cuadrado, se minimiza la suma de errores absolutos. Este método es equivalente a estimar una regresión de cuantiles en la mediana de la distribución. Lo anterior implica que la línea de regresión, en vez de pasar por la media condicional de los datos, pasará por la mediana condicional. Este tipo de regresión es de gran utilidad, principalmente por la aplicación que se describe a continuación.
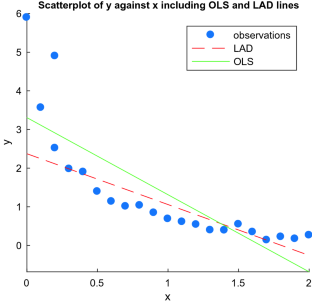
Regresión en presencia de outliers
La regresión lineal no es una buen método para estimar la relación entre un grupo de variables en presencia de valores atípicos (outliers), debido a que no es un método robusto. Los valores atípicos son valores extremadamente pequeños o grandes en comparación al resto de la distribución de los datos. En este contexto, un método poco robusto es uno cuyas estimaciones varían demasiado dependiendo de la inclusión o exclusión de los valores atípicos, es decir, se trata de un método que no entrega estimaciones precisas de la relación entre las variables en presencia de outliers. Por el contrario, se dice que un método es robusto cuando la estimación depende poco de la muestra que se esté utilizando. La regresión de cuantiles destaca en este aspecto por ser un método robusto, que no es influenciado significativamente por la presencia de valores atípicos.
Comentarios finales
La regresión de cuantiles es una gran herramienta para el análisis econométrico, ya que permite profundizar en el estudio de las relaciones entre variables, de forma de revelar relaciones que no son evidentes al enfocarse sólo en los promedios. Por otro lado, las regresiones de cuantiles destacan por ser métodos robustos, que no son afectados por la presencia de valores atípicos, que en el caso de la regresión lineal afectan en gran manera la precisión de las estimaciones.