Medidas de evaluación de modelos de clasificación y datos desbalanceados
Contenidos
Para evaluar cómo se están desempeñando nuestros algoritmos, existe una serie de medidas o métricas ampliamente utilizadas que, no obstante, nos pueden llevar a realizar conclusiones equivocadas. Un caso importante se da en los problemas de clasificación, cuando tenemos una base de datos desbalanceada, en que existe una clase minoritaria en la variable dependiente. En otras palabras, cuando la variable de respuesta tiene una distribución desigual entre sus clases. En dicho caso, el algoritmo no recibe suficiente información de la clase minoritaria como para hacer una buena predicción.
Ejemplos de variables dependientes desbalanceadas
Un sistema automático detecta fallas en un proceso de manufactura. Resulta que el número de casos defectuosos es significativamente menor al número de casos no defectuosos. Otro caso se da en la detección de fraude en transacciones con tarjetas de crédito, el número de transacciones fraudulentas es mucho menor que las transacciones no fraudulentas. En casos como esto, el desempeño de un algoritmo de machine learning estará sesgado hacia la clase mayoritaria, ya que minimizar los errores de predicción en la clase minoritaria contribuye muy poco a mejorar el desempeño en general del algoritmo. Por ejemplo, si sólo el 1% de las transacciones con tarjetas de crédito son fraudulentas, un algoritmo puede predecir que todas las transacciones serán no fraudulentas, y logrará un 99% de precisión.

Cómo resolver el problema de los datos desbalanceados
Rebalancear la muestra es uno de los métodos más comunes para resolver el problema de los datos desbalanceados. Una primera alternativa es disminuir la cantidad de ejemplos de la clase mayoritaria (undersampling), para que exista un menor desbalance entre las clases. Sin embargo, con este método se pierde información de la clase mayoritaria, que puede ser importante para el proceso de aprendizaje. Alternativamente, se puede tomar una mayor cantidad de ejemplos de la clase minoritaria (oversampling), caso en que habría ejemplos repetidos, lo que puede producir overfitting. Una tercera alternativa es generar datos sintéticos para la clase minoritaria, mediante algún método apropiado para la tarea, lo que generalmente produce mejores resultados que los métodos anteriores. Por último, se puede optimizar el algoritmo en base a medidas de precisión que tomen en cuenta el desbalance de los datos.
Cómo medir la precisión de las predicciones de un algoritmo: la matriz de confusión
La matriz de confusión es un cuadro que permite visualizar el desempeño de un algoritmo de clasificación en base a un conjunto de métricas. Muestra la siguiente información:
True Negatives (TN): valores que el modelo predice como NEGATIVOS, y que efectivamente son NEGATIVOS.
True Positives (TP): valores que el modelo predice como POSITIVOS, y que efectivamente son POSITIVOS.
False Negatives (FN): valores que el modelo predice como NEGATIVOS, pero que efectivamente son POSITIVOS.
False Positives (FP): valores que el modelo predice como POSITIVOS, pero que efectivamente son NEGATIVOS.
| Valores Efectivos | ||
| Predicción | POSITIVO | NEGATIVO |
| POSITIVO | TN | FN |
| NEGATIVO | FP | TP |
A partir de la matriz de confusión se puede calcular una métrica de costo total:
Costo total = C(FN) + C(FP)
Donde C(FN) es una función de costo asociada a los falsos negativos, y C(FP) es una función de costo asociada a los falsos positivos.
Además del costo total, existe una gran variedad de métricas que se obtienen a partir de la matriz de confusión, incluyendo las medidas más utilizadas, que son Accuracy y Error rate. A continuación, se describen las métricas más importantes.
Accuracy: (TP + TN)/(TP + TN + FP + FN)
Accuracy es una medida que muestra la suma de predicciones correctas (POSITIVOS y NEGATIVOS) sobre el total de predicciones.
Error Rate = 1 – Accuracy = (FP + FN)/(TP + TN + FP + FN)
La tasa de error es el número de predicciones incorrectas (POSITIVOS y NEGATIVOS) sobre el total de predicciones.
Precision = TP / (TP + FP)
Muestra qué porcentaje de las observaciones clasificadas como positivas por el modelo (TP + FP), son efectivamente positivas (TP). Un modelo con alta precisión es un modelo con pocos falsos positivos (falsa alarma).
Recall = Sensitivity = TP / (TP + FN)
Muestra qué porcentaje de las observaciones efectivamente positivas (TP + FN), fueron clasificadas como positivas por el modelo (TP). Un modelo con alto recall es un modelo con pocos falsos negativos, es decir, un modelo que clasifica correctamente la mayoría de los casos efectivamente positivos.
Las métricas más adecuadas, aquellas que combinan otras métricas
F1 score
Es una medida de precisión que se elabora tomando la media harmónica de las dos medidas anteriores (Precision & Recall). Toma su mejor valor en 1 y su peor valor en 0.

En esta versión del indicador se le da igual importancia a ambos indicadores, Precision & Recall, aunque se puede modificar la fórmula para dar mayor importancia a alguno de los dos. Esta métrica es útil debido a que existe un tradeoff entre precisión y recall. Las dos medidas son importantes, y en muchos casos es decisión del investigador optimizar una medida o la otra. Sin embargo, si se quiere tener una única medida para cuantificar el desempeño de un modelo, éste es un buen indicador.
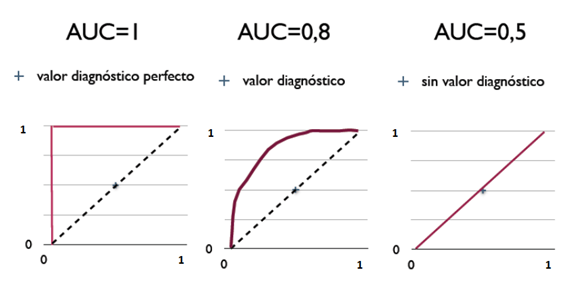
ROC curve (Receiver Operating Characteristic)
Es un gráfico que permite visualizar la capacidad de un modelo de clasificación en distintos umbrales de discriminación. Los algoritmos de clasificación típicamente entregan una probabilidad, es decir, un valor continuo entre 0 y 1. El umbral de discriminación es el valor a partir del cual se considera la predicción como positiva (1) o negativa (0). Generalmente se usa el valor 0.5, es decir, cualquier probabilidad mayor a 0.5 produce una clasificación positiva, que es un valor igual a 1 en la predicción, y cualquier probabilidad menor a 0.5 produce una clasificación negativa, es decir, un valor igual a 0 en la predicción. No obstante, el umbral se puede modificar dependiendo del tipo de error cuya minimización sea más importante para el investigador. La curva se elabora graficando la TRUE POSITIVE RATE (Recall o Sensitivity) sobre la FALSE POSITIVE RATE (Specificity) para distintos umbrales de clasificación.
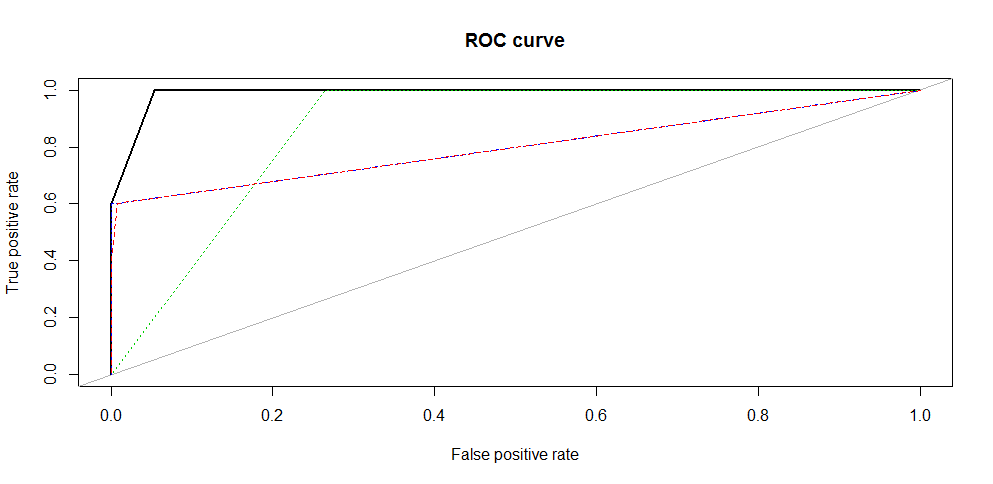
ROC AUC (Area under the curve)
Área bajo la curva ROC. Se puede interpretar como la probabilidad de que un algoritmo clasificador asigne una mayor probabilidad a una observación clasificada como positiva, que fue seleccionada aleatoriamente, que a una observación clasificada como negativa seleccionada aleatoriamente. Los valores que puede tomar esta área varían entre 0.5 y 1, donde 1 representa un clasificador perfecto, y 0.5 es un clasificador sin capacidad discriminatoria. Este es un buen indicador para evaluar un algoritmo de clasificación.

Conclusión
Las medidas más utilizadas para evaluar algoritmos de clasificación son Accuracy y Error Rate, sin embargo, estas medidas no son las más adecuadas cuando la variable dependiente está desbalanceada, ya que los resultados obtenidos para la clase minoritaria tienen una influencia muy pequeña en los indicadores. En este caso, las medidas como Precision, Recall y F1 score son las más adecuadas. Por otra parte, la curva ROC y, en particular, el área bajo la curva, AUC, es considerado el indicador más fiable de la precisión de un modelo, y es el más ampliamente utilizado para comparar el desempeño de modelos alternativos.